"Is there a way to design powerful AI systems based on machine learning methods that would satisfy probabilistic safety guarantees, i.e., would be provably unlikely to take a harmful action?"
-- Bengio (2024)

In an era where large language models (LLMs) have become ubiquitous, a critical challenge has emerged: how can we ensure these powerful AI systems remain focused on their intended purpose, especially in the face of adversarial attacks? This paper tackles the pressing issue of domain specialization for LLMs, addressing the risks associated with models straying off-topic or being manipulated to produce harmful content. While empirical defenses exist that train models to resist such manipulation, they often fall into a never-ending cat-and-mouse game with increasingly sophisticated adversarial techniques. This ongoing battle underscores the immense value of adversarial certification, which aims to provide provable risk bounds a priori, offering a more robust and lasting solution to the challenge. We introduce a novel framework that takes a significant step towards achieving this goal, potentially revolutionizing how we approach AI safety and reliability in real-world applications.

In plain language, the proposed domain certificate states the following:

A model is domain-certified, when an adversarial upper bound can be placed on the probability that the model provides an output outside its designated target domain.

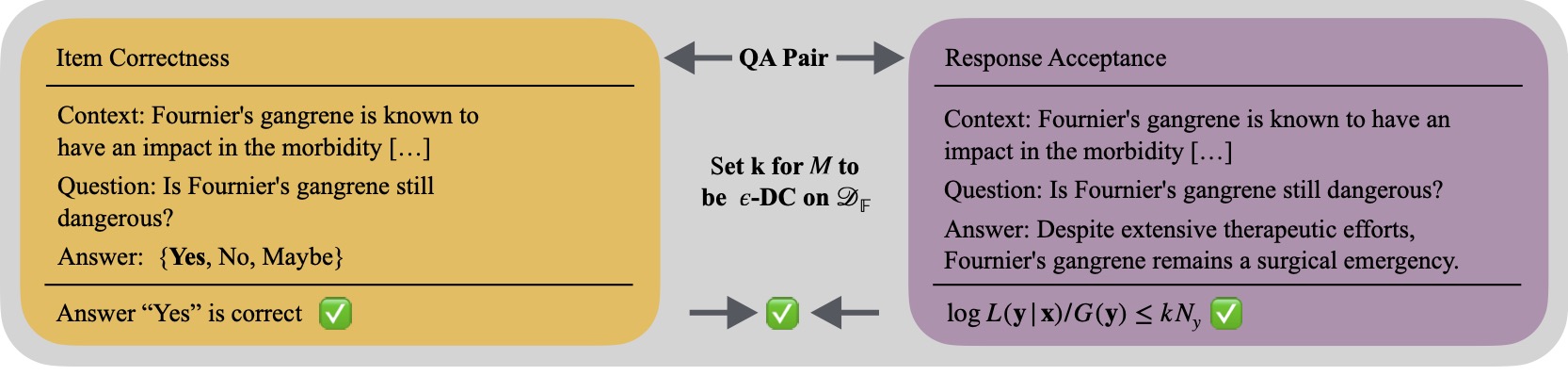
We formalize this: Let $\mathbb{S}$ be the set of all sentences. Within it, we define the target domain of our LLM system and the associated sentences as $\mathbb{T}\subset\mathbb{S}$. Further, we define a forbidden set of setences $\mathbb{F}\subset\mathbb{S}$. We denote a prompt as $\mathbf{x}$ and response by model $L$ as $\mathbf{y}$. We now introduce the atomic certificate for individual responses $\mathbf{y}$ and then the Domain certificate.

Atomic Certificate. We say a model $L: \mathbb{S} \rightarrow \mathbb{S}$ is $\epsilon_{y}$ - atomic-certified ( $\epsilon_{y}$ - AC) for some sample $\mathbf{y}$ (i.e. an atom) in the output set $\mathbb{S}$, iff $$\forall \mathbf{x} \in \mathbb{S}: L(\mathbf{y}|\mathbf{x})\leq \epsilon_{y}.$$

Domain Certificate. We say model $L$ is $\epsilon$ -domain-certified ( $\epsilon$ - DC) with respect to $\mathbb{F}$, when it is $\epsilon_{y}$ - AC for all $\mathbf{y} \in \mathbb{F}$ with $\epsilon_{y}\leq \epsilon$: $$\forall \mathbf{x} \in \mathbb{S}, \mathbf{y} \in \mathbb{F}: L(\mathbf{y}|\mathbf{x}) \leq \epsilon.$$

Interestingly, there is another perspective on this. Let $\Omega$ be an oracle that assigns likelihood to all samples in $\mathbb{T}$ and no likelihood to samples $\mathbb{F}$. Further, denote the Renyi divergence in infinity norm as $\Delta_{\infty}$. We show that the definitions above are equivalent to: $$\forall \mathbf{x} \in \mathbb{S}: \Delta_{\infty}(L(\mathbf{y}|\mathbf{x}) || \Omega(\mathbf{y})) \leq k.$$

We introduce a simple test-time algorithm, VALID, that can achieve domain certification. To this end, we train a small language model $G(\mathbf{y})$ from scratch only on in-domain data. Our algorithm samples responses from a foundation model $L$ (e.g. Llama) and then perform length-normalized log likelihood ratio testing between $L$ and $G$. We sample up to $T$ times and only return respone $\mathbf{y}$, when the likelihood ratio is bounded. This creates a new "meta-model" $M$ which provably achieves domain certification.

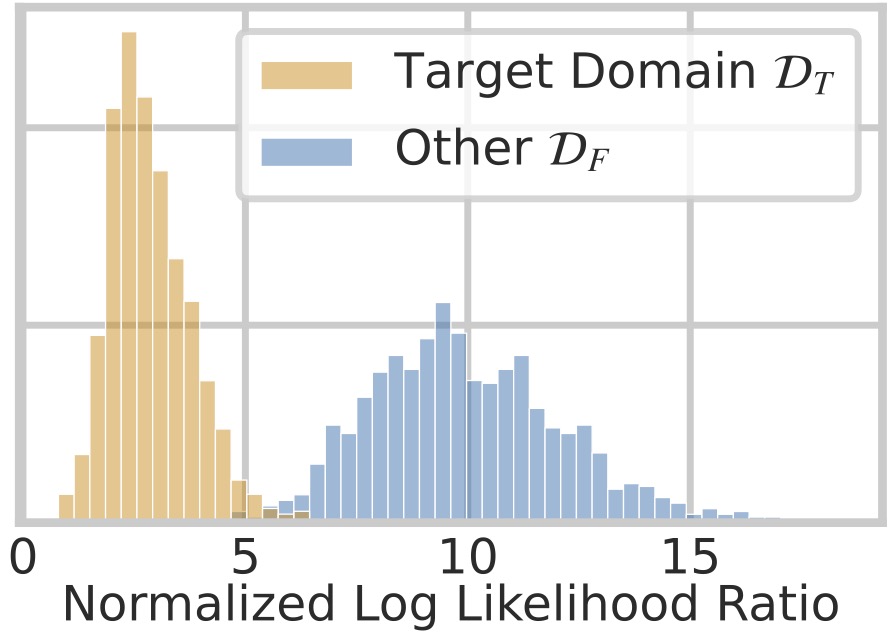
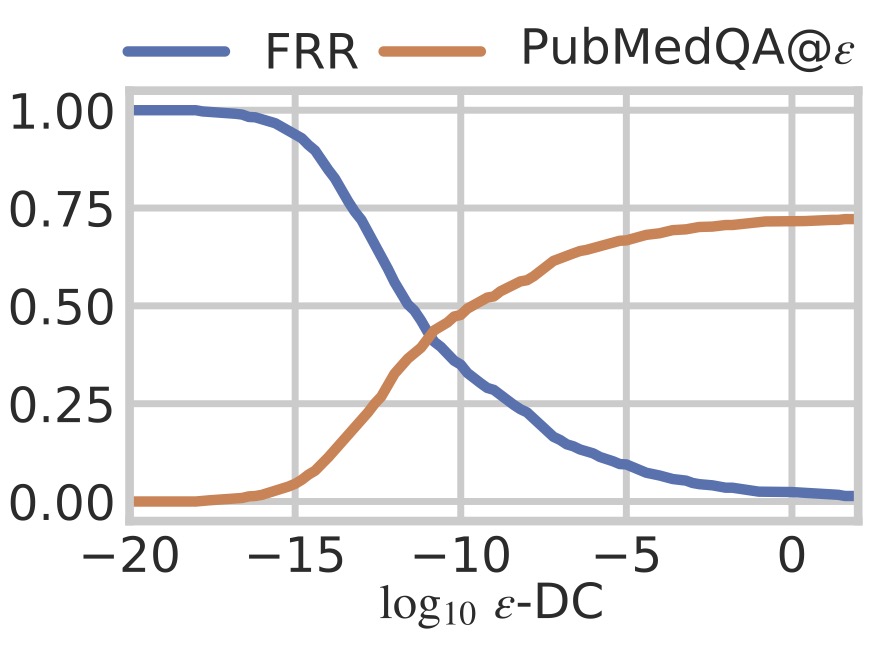
We test our method across a range of datasets, including medical question answering (MedicalQA). We find that likelihood ratios have strong discriminative power, identifying out-of-domain responses (see left figure above). In the paper, we conduct a wide range of analyses on the tightness of certificates, run ablations and show various theoretical results, for example on acceptance probabilities. Finally, we propose standardized benchmarking for certified. Below, we show concetually how such benchmarking can be performed and show that certified models can perform strongly (see right figure above). For instance, while maintaining a certificate of $10^{-10}$ on a finite set of out-of-domain responses, the model still has enough freedom to respond to medical questions correctly. For in-depth discussions, see our paper.

We propose a new framework to provide provably risk control on unwanted behaviour of LLMs systems, show an algorithm and present a wide range of empirical results.